Taylor and Maclaurin Series: Exercises and Solutions



Taylor series representation of a function

Notation:
$$f^{(n)}(x) = \frac{d^n f}{dx^n}(x)$$
Taylor series for \( f(x) \) about the point \( x_0 \):
$$f(x) = \sum_{n=0}^{\infty} \frac{(x - x_0)^n}{n!} f^{(n)}(x_0)$$
$$f(x) = f(x_0) + (x - x_0)\frac{df}{dx}(x_0) + \frac{(x - x_0)^2}{2}\frac{d^2 f}{dx^2}(x_0) + \frac{(x - x_0)^3}{3!}\frac{d^3 f}{dx^3}(x_0) + \dots$$
Maclaurin series (special case where \( x_0 = 0 \)):
$$f(x) = f(0) + x\frac{df}{dx}(0) + \frac{x^2}{2}\frac{d^2 f}{dx^2}(0) + \frac{x^3}{3!}\frac{d^3 f}{dx^3}(0) + \dots$$

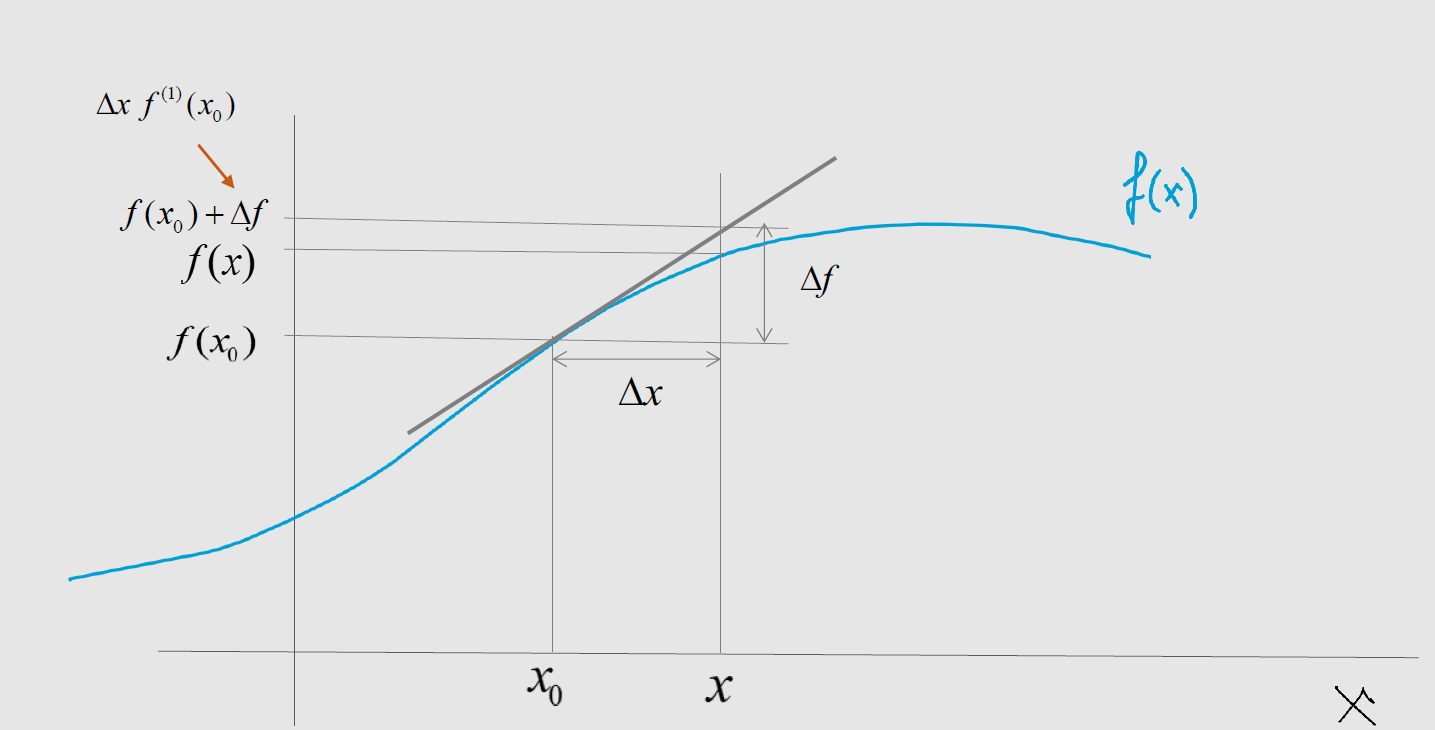
Taylor series: interpretation

$$f(x_0 + \Delta x) \approx f(x_0) + \Delta x \, f^{(1)}(x_0) + \frac{1}{2}\Delta x^2 \, f^{(2)}(x_0) + \frac{1}{3!}\Delta x^3 \, f^{(3)}(x_0) + \dots$$
Image of a Taylor Series

Finding the Maclaurin series for the exponential function

Function:
$$f(x) = e^x$$
Series:
$$f(x) = \sum_{n=0}^{\infty} \frac{x^n f^{(n)}(0)}{n!}$$
Table of Terms:
n \( f^{(n)}(x) \) \( f^{(n)}(0) \) \( \frac{x^n}{n!} \)
0 \( e^x \) 1 1
1 \( e^x \) 1 x
2 \( e^x \) 1 \( \frac{x^2}{2} \)
3 \( e^x \) 1 \( \frac{x^3}{3!} \)
... ... ... ...
Put the terms together:
$$e^x = 1 + x + \frac{x^2}{2} + \frac{x^3}{3!} + \dots$$

Visualising partial sums of Maclaurin series

$$e^x = 1 + x + \frac{x^2}{2} + \frac{x^3}{3!} + \dots$$
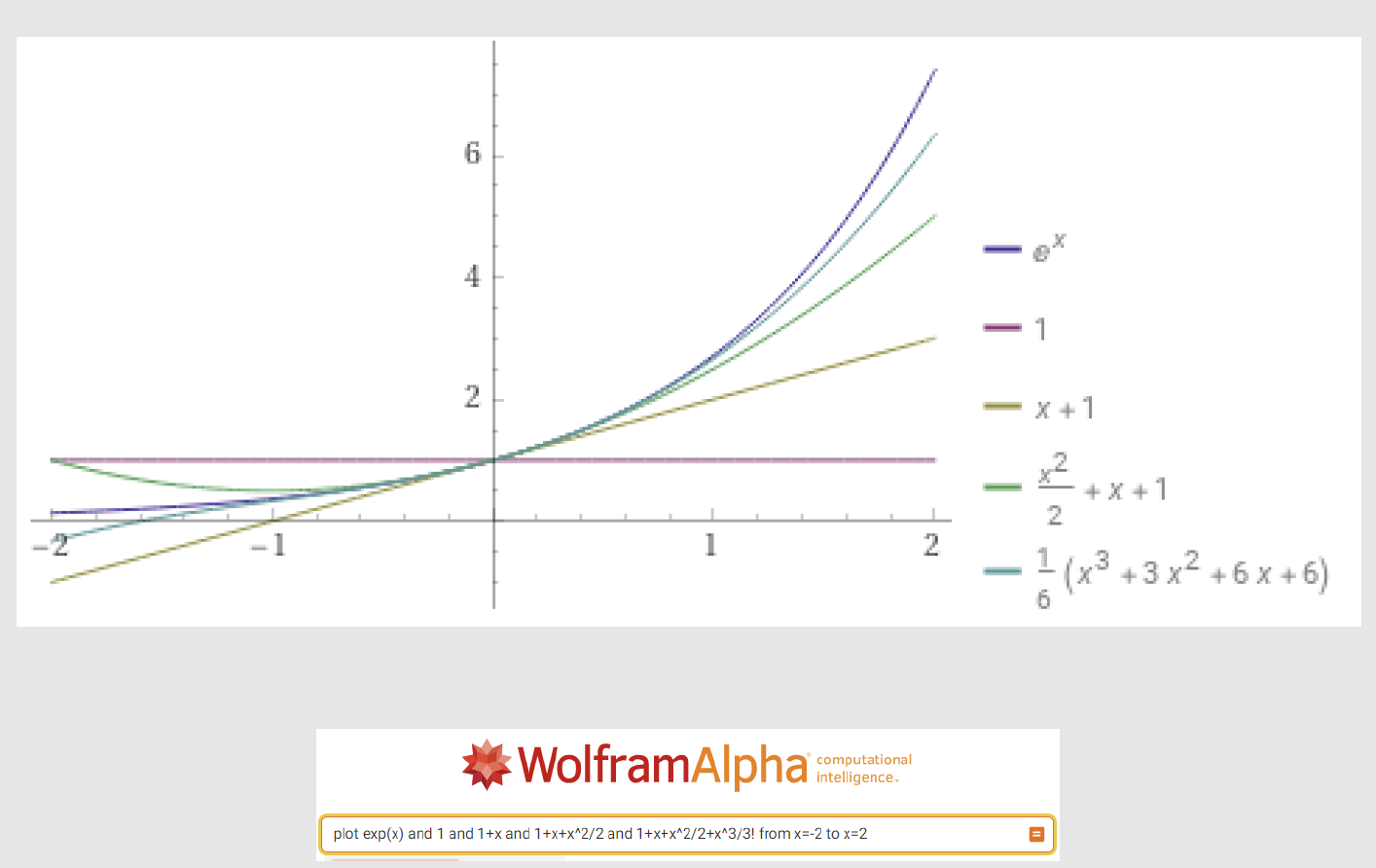
Image of partial_sums_taylor_series

Approximating a function using partial sums

Function:
$$e^x = 1 + x + \frac{x^2}{2} + \frac{x^3}{3!} + \dots$$
Partial sum:
$$S_N(x) = \sum_{n=0}^{N} \frac{x^n f^{(n)}(x)}{n!}$$
Choose x=0.5 (for illustration)
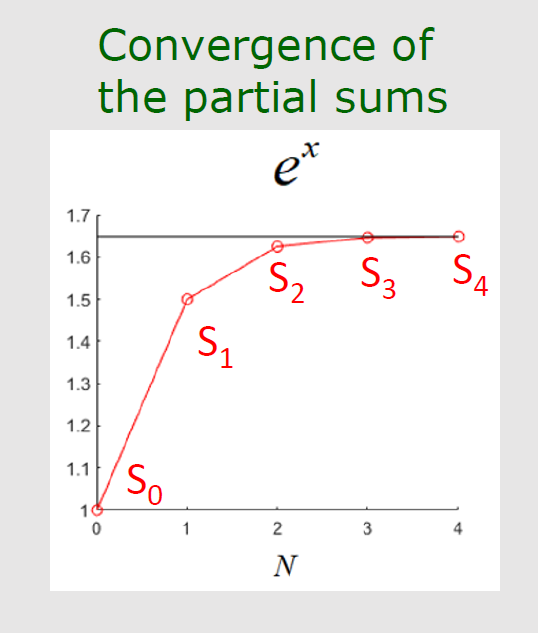
Image of pconvergence_partial_sums_taylor_series

Convergence of the Maclaurin series for the exponential function

$$e^x = 1 + x + \frac{x^2}{2} + \frac{x^3}{3!} + \dots$$
Choose x=0.5

Matlab code:

x = .5;
for N=0:15
ss=0;
for n=0:N
ss = ss +
x.^n./factorial(n);
end
fprintf('%d, %f, %f,%e\n',N,ss,exp(x),exp(x)-ss)
end
N \( S_N \) \( \exp(x) \) \( \exp(x) - S_N \)
011.6487216.49E-01
11.51.6487211.49E-01
21.6251.6487212.37E-02
31.6458331.6487212.89E-03
41.6484381.6487212.84E-04
51.6486981.6487212.34E-05
61.648721.6487211.65E-06
71.6487211.6487211.03E-07
81.6487211.6487215.66E-09
91.6487211.6487212.82E-10
101.6487211.6487211.28E-11
111.6487211.6487215.30E-13
121.6487211.6487212.07E-14
131.6487211.6487211.11E-15
141.6487211.6487214.44E-16
151.6487211.6487214.44E-16



Approximation error

$$e^x = 1 + x + \frac{x^2}{2} + \frac{x^3}{3!} + \dots$$

Truncation error:

$$E_N(x) = \lvert f(x) - S_N(x) \rvert$$

Truncation error from S15

$$E_{15}(0.5) \sim 10^{-16}$$

Examples of other Taylor series

$$\sin x = \sum_{n=0}^{\infty} (-1)^n \frac{x^{2n+1}}{(2n+1)!}$$
$$\cos x = \sum_{n=0}^{\infty} (-1)^n \frac{x^{2n}}{(2n)!}$$
$$\ln(1+x) = \sum_{n=1}^{\infty} (-1)^{n+1} \frac{x^n}{n}$$
$$\frac{1}{1-x} = \sum_{n=0}^{\infty} x^n$$



Solution of practice problems



Determine the Maclaurin series for cos(x)

View the solution


Determine the Maclaurin series for ln(1+x)

View the solution


Calculate the Taylor expansion of cos(x) around the point x0 = ℼ/2

The Taylor formula is

$$f(x) = \sum_{n=0}^{\infty} \frac{(x - \pi/2)^n}{n!} f^{(n)}\!\left(\frac{\pi}{2}\right)$$ View the solution


Use the Maclaurin series for ln((1+x) to calculate the limit limx→0 ln(1 + x)⁄x

View the solution



4√17

View the solution



3√26

View the solution