Fourier Series Analysis: Exercises and Solutions

Fourier series for a function in the interval -π ≤ x ≤ π

$$f(x) = \frac{a_0}{2} + \sum_{n=1}^{\infty} a_n \cos(nx) + \sum_{n=1}^{\infty} b_n \sin(nx)$$

Fourier coefficients:

$$a_0 = \frac{1}{\pi} \int_{-\pi}^{\pi} f(x) \, dx,$$
$$a_n = \frac{1}{\pi} \int_{-\pi}^{\pi} f(x) \cos(nx) \, dx,$$
$$b_n = \frac{1}{\pi} \int_{-\pi}^{\pi} f(x) \sin(nx) \, dx.$$


Example: Find the Fourier series for the function f(x) = x

View the solution


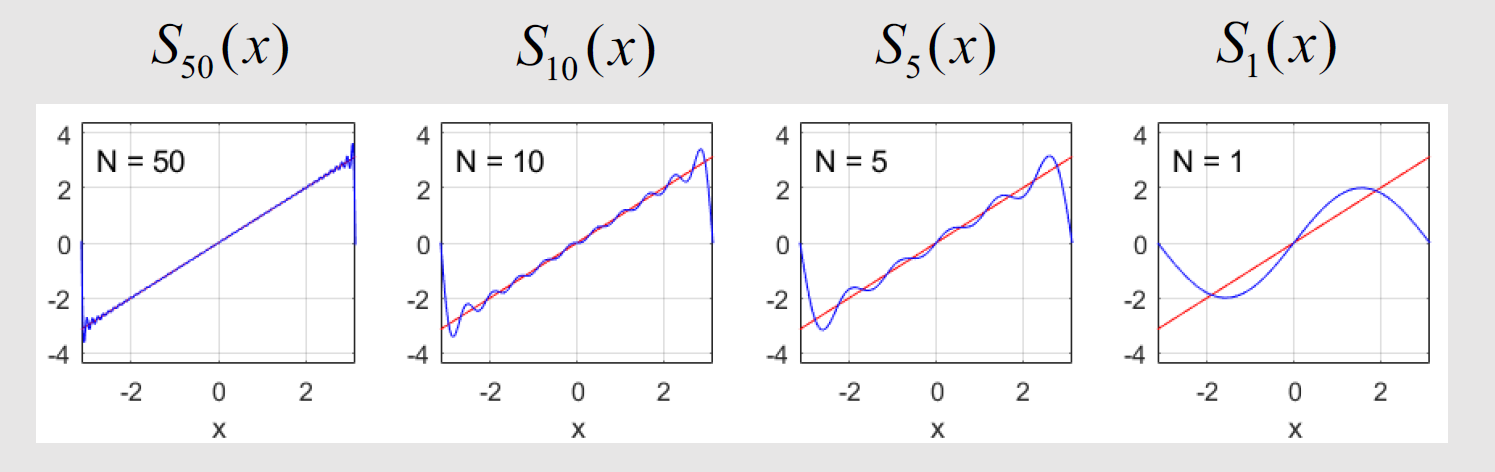
Approximating a function using a finite sum of the Fourier series: f(x) ≈ SN(x)

$$f(x) = \frac{a_0}{2} + \sum_{n=1}^{\infty} a_n \cos(nx) + \sum_{n=1}^{\infty} b_n \sin(nx)$$

Example: F(x) = x

Image of Fourier f(x) = x

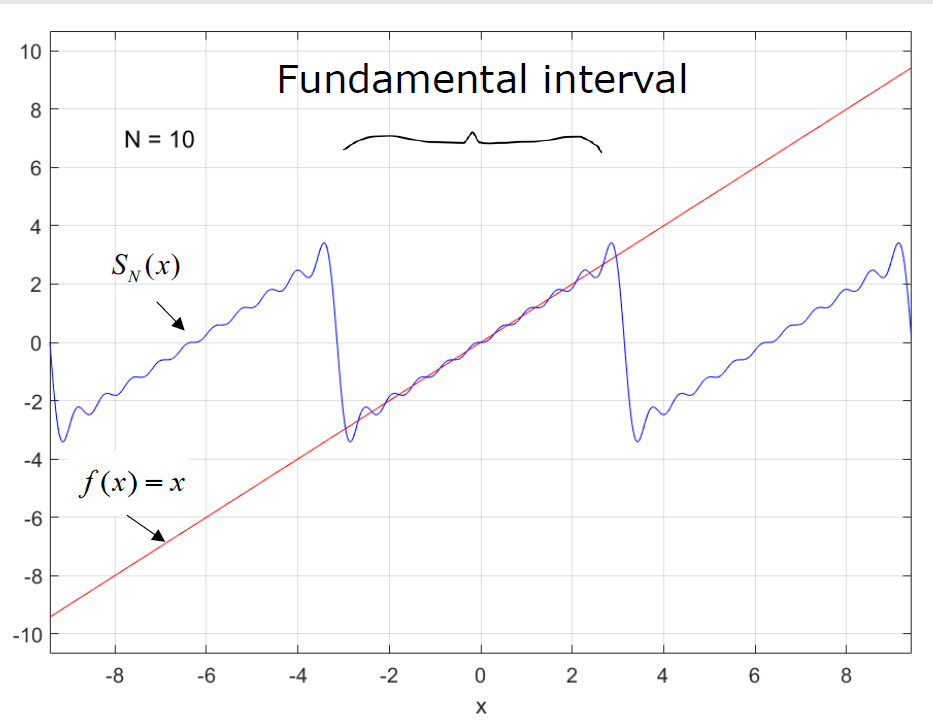
The Fourier series of a function converges on its periodic extension

function converges on its periodic extension

Odd and even functions

Type Definition Example Fourier Coefficients
Odd function \( f(-x) = -f(x) \) \( x^3 \) \( a_0 = 0,\ a_n = 0 \)
Even function \( f(-x) = f(x) \) \( x^2 \) \( b_n = 0 \)

Facts:

$$f(x) = \frac{1}{2} f(x) + \frac{1}{2} f(x)$$
$$f(x) = \frac{1}{2} f(x) \hspace{4cm} + \frac{1}{2} f(x)$$
$$f(x) = \frac{1}{2} f(x) + \frac{1}{2} f(-x) \hspace{4cm} + \frac{1}{2} f(x) - \frac{1}{2} f(-x)$$
$$f(x) = \underbrace{\frac{1}{2}\big(f(x)+f(-x)\big)}_{\textstyle f^{\text{EVEN}}(x)} \hspace{4cm} + \underbrace{\frac{1}{2}\big(f(x)-f(-x)\big)}_{\textstyle f^{\text{ODD}}(x)}$$

Fourier Series Practice Exercises

Exercise 1: Given the function f(x) = |x| − π/2

Question 1

a) Determine if the function is odd or even or neither, and based on that decide which,
if any, of the Fourier coefficients vanish.

View the solution


Question 2

b) The Fourier series for this function in the fundamental interval \( -\pi < x < \pi \) is given as:

$$\frac{2}{\pi} \sum_{n=1}^{\infty} \frac{1}{n^2} \Big[(-1)^n - 1\Big] \cos(nx)$$

Write this series term-by-term by explicitly showing only the first three non-zero terms, replacing the rest by the ellipsis "..."

View the solution


Question 3

c) Calculate the truncation errors associated with this series at the value x = π/3, for finite
sums containing only the first one, two and three non-zero terms.

View the solution


Question 4

d) Sketch the function and its periodic extensions.

View the solution


Use plotting software to plot the finite sum consisting of the first three non-zero terms.

View the solution


Exercise 2: Given the function f (x) = x3

Question 1

a) Determine if the function is odd or even or neither, and based on that decide which, if any,
of the Fourier coefficients vanish.

View the solution


Question 2

The Fourier series for this function in the fundamental interval \( -\pi < x < \pi \) is given as:

$$2 \sum_{n=1}^{\infty} \Big[ (-1)^n \big(6 - n^2 \pi^2\big) / n^3 \Big] \sin(nx)$$
View the solution


Question 3

Calculate the truncation errors associated with this series at the value x = 0.8, for finite
sums containing only the first one, two and three non-zero terms.

View the solution


View the comparison of f(x) with the 3-term Fourier series plotted using Wolfram Alpha: