Vectors: Exercises and Solutions
A vector can represent the state of a system as a point in state space.
The point moves along a trajectory generated by the dynamics of the system.
The dynamics is typically represented by differential equations.
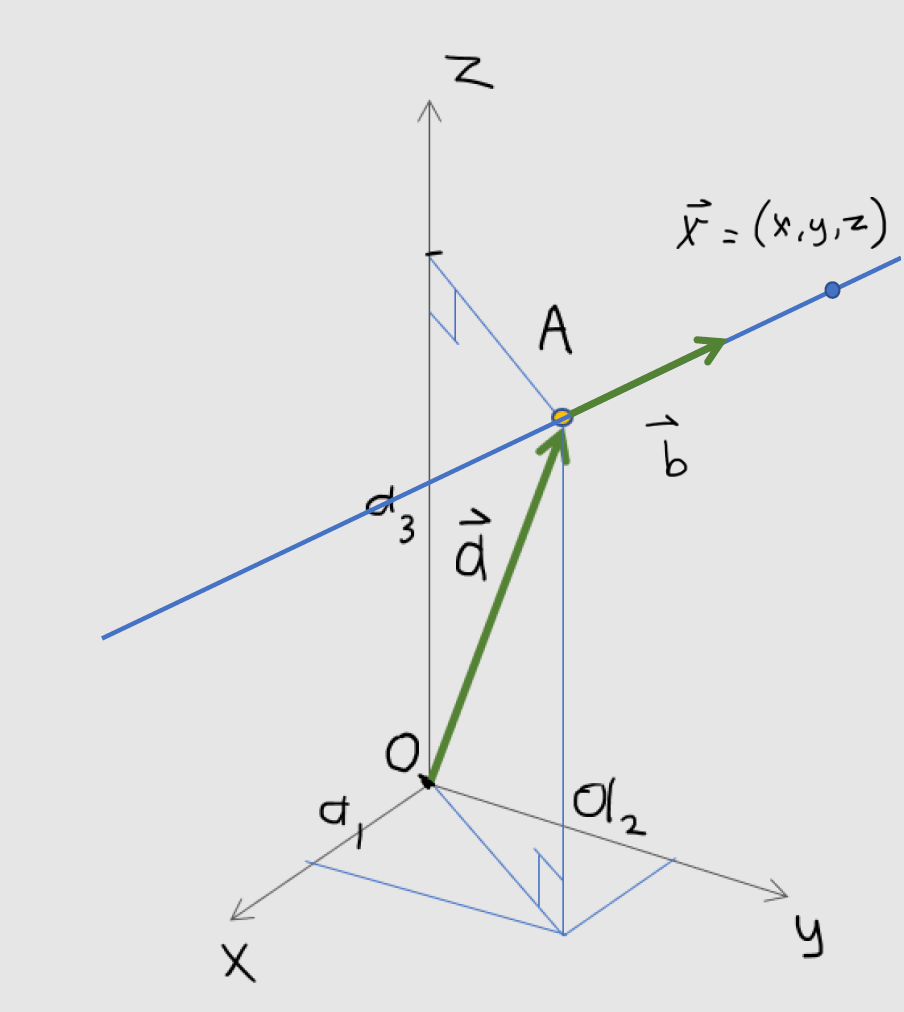
Line
Vector equation for the line:
Corresponds to 3 scalar equations:
(Assume none of \( b_1, b_2, b_3 \) is zero)
Cartesian equations for the line:
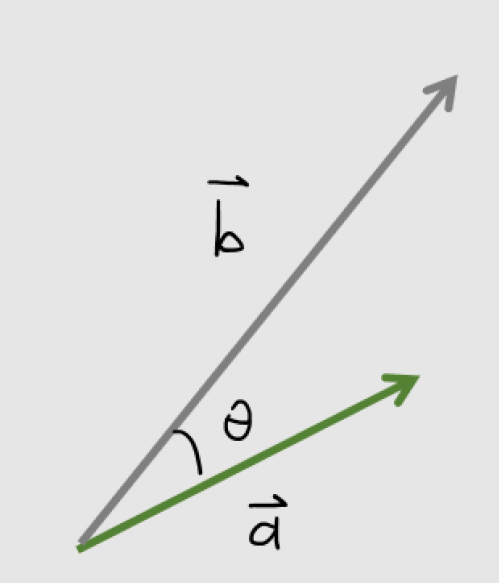
Dot product (scalar product)
Given two vectors a and b, there is a unique angle 0 ≤ θ <π between them.
Definition of the dot product:
Its properties:
- $$\vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a}$$
- $$\vec{a} \cdot (\vec{b} + \vec{c}) = \vec{a} \cdot \vec{b} + \vec{a} \cdot \vec{c}$$
- $$(k \vec{a}) \cdot \vec{b} = k (\vec{a} \cdot \vec{b})$$
In addition
Since \(\hat{i} \cdot \hat{i} = \hat{j} \cdot \hat{j} = \hat{k} \cdot \hat{k} = 1\) and all other dot products are zero:
The angle between two vectors
Derivation of the formula for the angle between two vectors:
Compute \(\cos \theta\):
Projection
Derivation of the formula for the projection of b along the direction of a
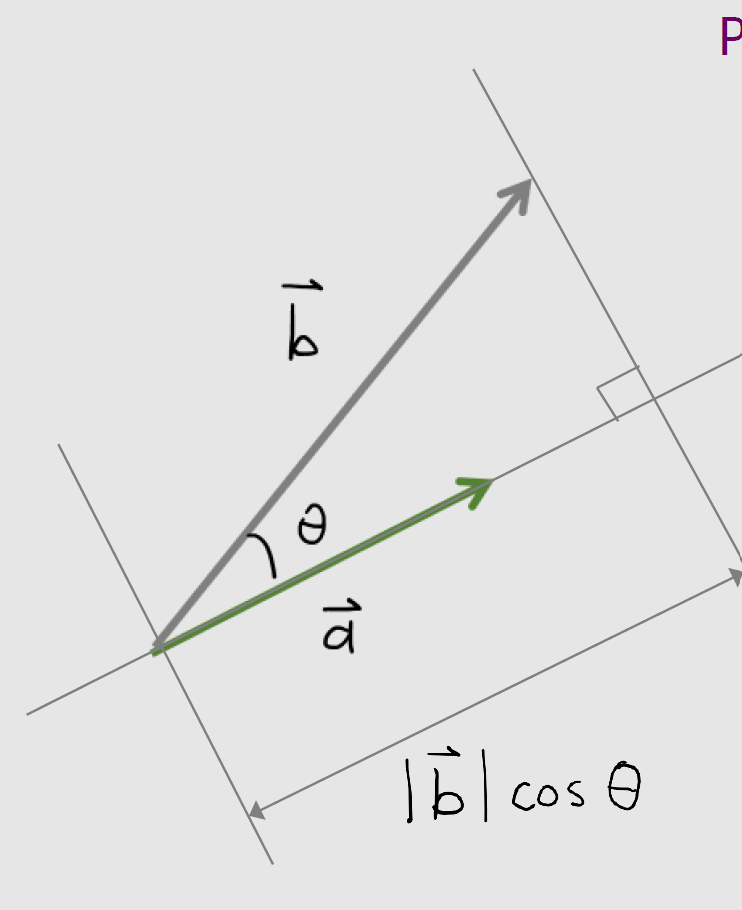
$$\vec{a} \cdot \vec{b} = |\vec{a}| |\vec{b}| \cos\theta$$
$$|\vec{b}| \cos\theta = \dfrac{\vec{a} \cdot \vec{b}}{|\vec{a}|}$$
$$|\vec{b}| \cos\theta = \vec{b} \cdot \left( \dfrac{\vec{a}}{|\vec{a}|} \right)$$
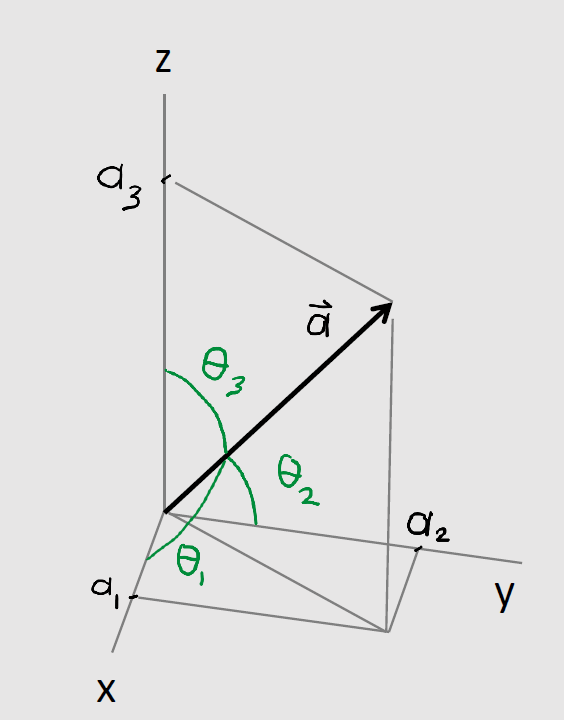
Direction cosines of a vector
$$\cos\theta_1 = \frac{a_1}{|\vec{a}|}$$

Direction cosines of a vector are the cosines of the angles between the vector and each of the three coordinate axes.
They represent the direction of the vector by showing how much it “aligns” with each axis.
$$\cos\theta_1 = \frac{a_1}{|\vec{a}|}$$
$$\cos\theta_2 = \frac{a_2}{|\vec{a}|}$$
$$\cos\theta_3 = \frac{a_3}{|\vec{a}|}$$
Practice Exercises
Exercise 1
Given u = (1,2,3) and v = (0,1,2), calculate the vector projection of u along the direction of v.
The formula for vector projection is:
\( (\vec{u} \cdot \vec{v})\vec{v} \)
View the solutionExercise 2
Given the points A (1,-1,0) and B (2,1,2), determine the Cartesian equations for the line which contains A and B.
View the solutionExercise 3
What is the angle between the vectors u = (1,-1,0) and v = (2,1,2)?
View the solutionExercise 4
Given the vectors u = (2,-1,3) and v = (3,0,4), what is the vector projection of u in the direction of v?
View the solutionExercise 5
The points A (1,2,2), B (2,-1,0), C (4,5,-1) and D are located in 3-dimensional space at the
corners of a rectangle, with adjacent sides AB and AC. Find the coordinates of point D.
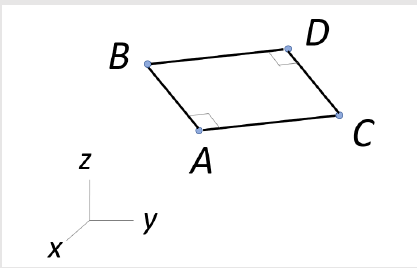 View the solution
View the solution
Exercise 6
Find the midpoint of the rectangle in the previous question.
View the solutionExercise 7
Write a set of Cartesian equations for the line that contains the point A (1,0,0) and is parallel to the vector b = (0,1,1).
View the solution