Multiple Integrals with Exercises and Solutions
The indefinite integral of function f(x) has an arbitrary constant of integration
$$g(x) = \int f(x)\,dx + \text{const}$$
An definite integral of function f(x) between limits A and B:
$$\int_{A}^{B} f(x)\,dx = g(B) - g(A)$$
Univariate Integration review
A definite integral of function f(x) between limits (bounds) A ≤ x ≤ B equals the area under the function:
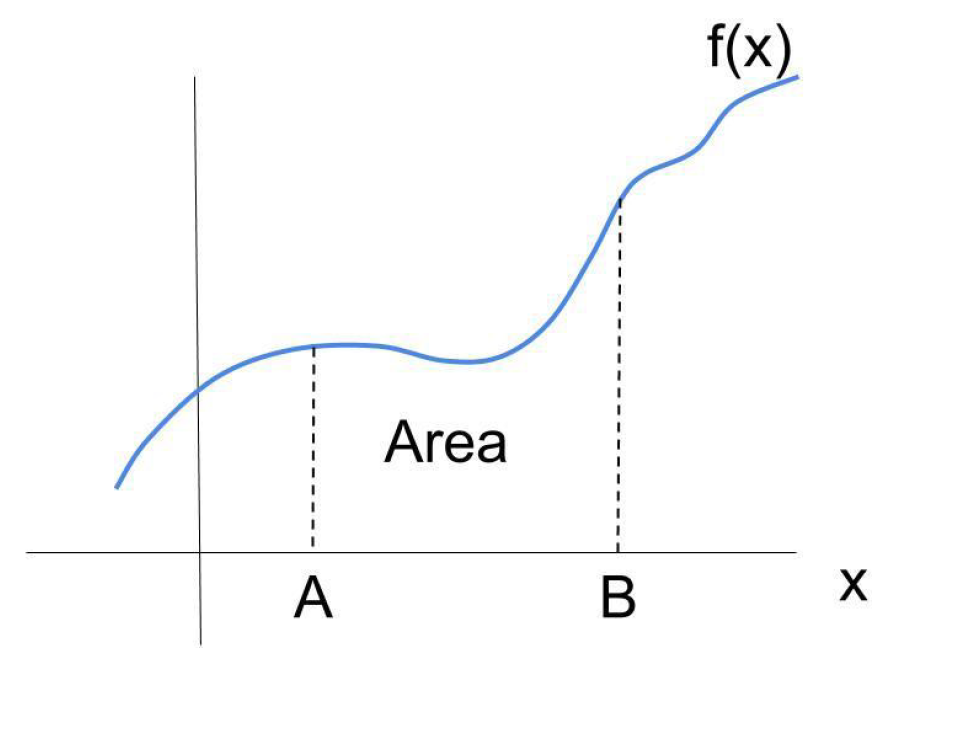
$$\text{Area} = \lim_{N \to \infty} \sum_{k=1}^{N} f(x_k)\,\Delta x$$
$$= \int_{A}^{B} f(x)\,dx$$
Multivariate Integration
Example of a definite integral of the multivariate function f(x,y) between the limits a ≤ x ≤ b and c ≤ y ≤ d:
$$I = \int_{y=c}^{y=d} \int_{x=a}^{x=b} f(x,y)\,dx\,dy$$
This is equivalent to two nested integrals:
$$I = \int_{y=c}^{y=d} \Bigg( \int_{x=a}^{x=b} f(x,y)\,dx \Bigg) dy$$
First do the “inner” integral for variable x, temporarily assuming that y is a constant. Then do the “outer” integral for y.
Order of integration:
In a definite integral:
If the limits are constants, the order of integration can be changed without changing the limits
If limits are functions of the variables of integration,
the order of integration may require modifications to the limits or to the integrals.
In an indefinite integral, the order of integration can always be changed.
Example 1: Calculate
$$I = \int_{y=0}^{y=1} \int_{x=1}^{x=2} x\,y^2 \, dx \, dy$$
Solution of Example 1:
$$I = \int_{y=c}^{d} \Bigg( \int_{x=a}^{b} x y^2 \, dx \Bigg) dy
= \int_{y=c}^{d} y^2 \Bigg[ \frac{x^2}{2} \Bigg]_{a}^{b} dy
= \int_{y=c}^{d} \frac{1}{2} y^2 (b^2 - a^2) \, dy
= \frac{1}{2}(b^2 - a^2) \Bigg[ \frac{y^3}{3} \Bigg]_{c}^{d}$$
$$= \frac{1}{6}(b^2 - a^2)(d^3 - c^3)
= \frac{1}{6}(2^2 - 1^2)(1^3 - 0^3)
= \frac{1}{6}(4 - 1)
= \boxed{\frac{1}{2}}$$
Multivariate Integration to find an area on the x-y plane
When f(x,y) = 1, the integral represents the area of the region in the xy plane.
Double Integral Example: Find
$$I = \int_{y=-1}^{2} \int_{x=2}^{3} \, dx \, dy$$
Solution of Double Integral Example:
$$I = \int_{y=-1}^{2} \Bigg( \int_{x=2}^{3} dx \Bigg) dy
= \int_{y=-1}^{2} x \Bigg|_{2}^{3} dy
= \int_{y=-1}^{2} (3 - 2) \, dy
= 1 \cdot y \Bigg|_{-1}^{2}$$
I = 2 - (-1) = 3
Example: Solve the integral and determine the region whose area is represented by the integral. Can you reverse the order of integration?
$$I = \int_{y=1}^{3} \int_{x=1}^{y} \, dx \, dy$$
Solution to the above example:
$$I = \int_{y=1}^{3} \Bigg( \int_{x=1}^{y} dx \Bigg) dy
= \int_{y=1}^{3} x \Bigg|_{1}^{y} dy
= \int_{y=1}^{3} (y - 1) \, dy
= \Bigg( \frac{y^2}{2} - y \Bigg) \Bigg|_{1}^{3}$$
$$= \Bigg( \frac{3^2}{2} - 3 \Bigg) - \Bigg( \frac{1^2}{2} - 1 \Bigg)
= \Bigg( \frac{9}{2} - 3 \Bigg) - \Bigg( \frac{1}{2} - 1 \Bigg)
= \Bigg( \frac{9 - 6}{2} \Bigg) - \Bigg( \frac{1 - 2}{2} \Bigg)
= \frac{3}{2} - \Bigg( -\frac{1}{2} \Bigg)
= 2$$
Example 1: Derivative of f(x) with respect to x:
\[
\frac{df}{dx}(x) = \lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x}
\]
Partial Differentiation
Partial derivative of f(x,y) with respect to x:
\[
\frac{\partial f}{\partial x}(x, y)
= \lim_{\Delta x \to 0}
\frac{f(x + \Delta x, y) - f(x, y)}{\Delta x}
\]
Partial derivative of f(x,y) with respect to y:
\[
\frac{\partial f}{\partial y}(x, y)
= \lim_{\Delta y \to 0}
\frac{f(x, y + \Delta y) - f(x, y)}{\Delta y}
\]
Example 1: Find the partial derivative with respect to x.
\[
f(x, y) = e^{-(x^{2} + y^{2})}
\]
View the solution
Example 2: Find the partial derivative with respect to x.
\[
f(x, y) = -(x-3)^{2} + xy + 16
\]
View the solution
Partial differentiation: Practical Questions
Example 3: Calculate all first and second order partial derivatives of:
\[
f(x, y) = e^{(3x^{2}y)}
\]
View the solution
Additional partial derivative with respect to x and y
Example 4:
\[
f(x, y) = x / y
\]
View the solution
Example 5:
\[
f(x, y) = - (x-3y)^{2}
\]
View the solution
Example 6:
\[
f(x, y) = e^{(2x+y^{3})}
\]
View the solution
Example 7:
\[
f(x, y) = xln(2y)
\]
View the solution
Example 8:
\[
f(x, y) = cos(x(e^{3x}))
\]
View the solution
Practice Exercises with Solutions
Exercise 1
$$I = \int_{y=-1}^{2} \int_{x=2}^{3} (x - y) \, dx \, dy$$
View the solution
Exercise 2
$$I = \int_{y=0}^{2} \int_{x=y}^{3} (x - y) \, dx \, dy$$
View the solution
Exercise 3
$$I = \int_{y=0}^{2} \int_{x=0}^{3} e^{x - y} \, dx \, dy$$
View the solution
Exercise 4
$$I = \int_{x=0}^{\pi} \int_{y=0}^{x} \sin(2x) \, dy \, dx$$
View the solution
Exercise 5
$$I = \int_{x=0}^{1} \int_{y=1}^{2} \frac{x}{y^2} e^{\frac{x}{y}} \, dy \, dx$$
View the solution
Exercise 6
$$I = \int_{s=0}^{\pi} \int_{t=0}^{s} s \cos(\pi - t) \, dt \, ds$$
View the solution